
- #Calculate fibonacci how to#
- #Calculate fibonacci mod#
- #Calculate fibonacci plus#
- #Calculate fibonacci series#
See The Mathematical Magic of the Fibonacci Numbers.
#Calculate fibonacci mod#
If the mod is 100, it finds the last 2 digits, if the mod is 1000 then the last 3 etc. This finds the remainder when G(a,b,i) is divided by the mod for your given value(s) of a, b and i. To find the final digits, use the button and supply the modulus in the input box. Option first (immediate results always) to see how many digits it has:
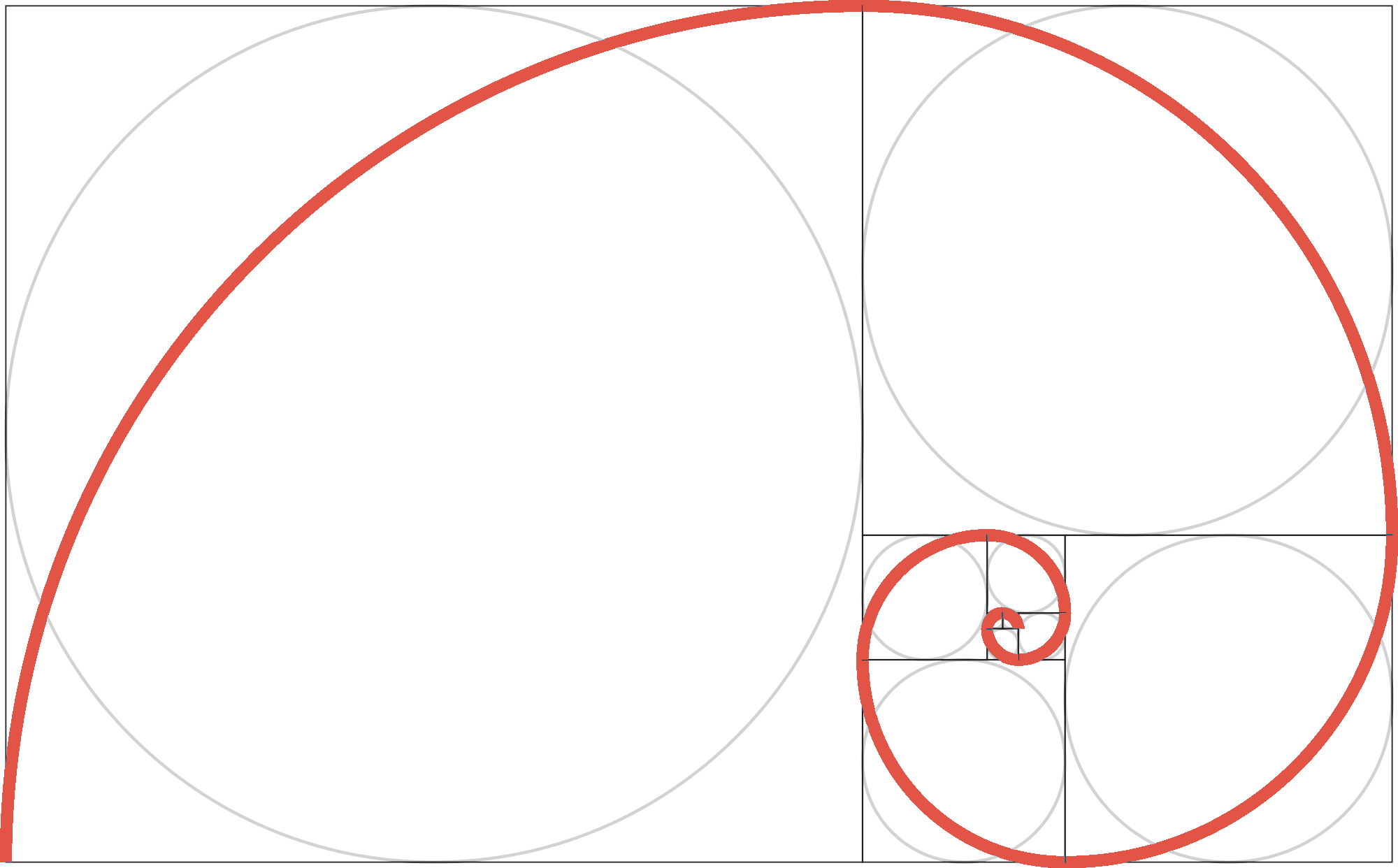
Tip: Always try the "approximate" or "the number of digits in" To compute (it may take longer on an older computer). For example F(1000) has 209 digits and will Take more time to calculate and your browser may appear to hang. The computations can be of extremely large numbers (many thousands of digits) and are exact but larger numbers and also toĬalculations can be exact with many decimal digits or approximations with the first few digits only being shown: This sequence of bits is related to the Powers of Phi, the golden ratio which is Phi = (√5 + 1)/2 = 1.6180339.Īnd phi = 1/Phi = Phi−1 = (√5 − 1)/2 = 0.6180339. the Rabbit Sequence, Rab(i) also called the Fibonacci Word and the Golden String Number which has n as a factor is called the Entry Point of n in that series. The Calculator on this page lets you examine this for any G series.Īlso every number n is a factor of some Fibonacci number. Has a section on the periodic nature of the remainders when we divide the Fibonacci numbers by any number (the modulus). Pisano periods and Entry points The Mathematics of the Fibonacci Numbers page Is ready for copying into a spreadsheet for further investigation. The output also shows the list of frequencies for first digits 1-9 or first two digits 10-99 which The Fibonacci, Lucas of General Fibonacci function in the given range of indices.
Yourself, shown as a frequency bar chart of the first one or the first two digits of
#Calculate fibonacci series#
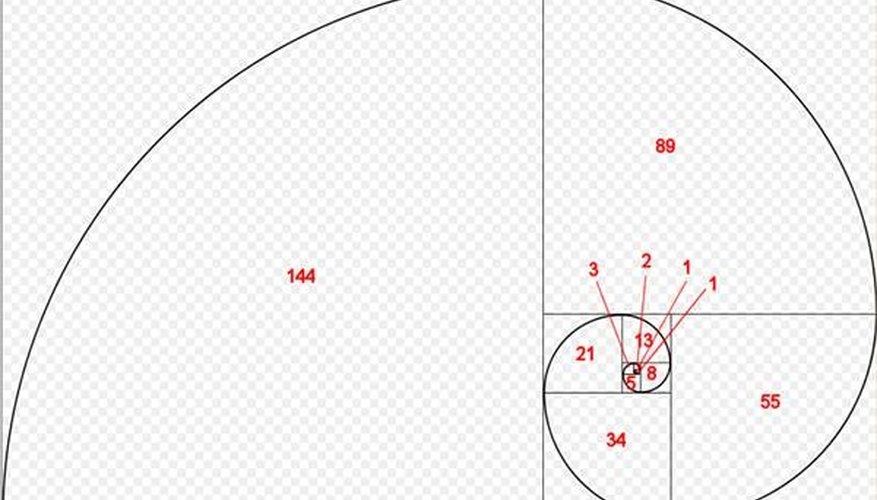
Here you can plot initial digits or the first two digits for a range of values in any G series and examine the data for 1 is the most popular, 2 is less popular through to the least popular initial digit: 9. Natural data (such as populations of countries and sizes of lakes) have a precise rule that determines how popular Benford's Law Plots Benford's Law states that the initial digit of many mathematical series as well as This is always exact for any index number i. exact remainders mod n finds the remainders on division by a given number n ("modulo n" or "mod n" for short). The number of digits Can compute the number of digits in huge G series numbers - see the previous section. The table below shows the first 100 numbers in the Fibonacci sequence.įirst 100 numbers in the Fibonacci sequence.G(0) = a, G(1) = b, G(a,b,n) = G(a,b,n-1) + G(a,b,n-2) for all integers n.
#Calculate fibonacci plus#
Thus, Binet’s formula states that the nth term in the Fibonacci sequence is equal to 1 divided by the square root of 5, times 1 plus the square root of 5 divided by 2 to the nth power, minus 1 minus the square root of 5 divided by 2 to the nth power.īinet’s formula above uses the golden ratio 1 + √5 / 2, which can also be represented as φ.įirst 100 Numbers in the Fibonacci Sequence

Named after French mathematician Jacques Philippe Marie Binet, Binet’s formula defines the equation to calculate the nth term in the Fibonacci sequence without using the recursive formula shown above.īased on the golden ratio, Binet’s formula can be represented in the following form:į n = 1 / √5(( 1 + √5 / 2) n – ( 1 – √5 / 2) n) Thus, the Fibonacci term in the nth position is equal to the term in the nth minus 1 position plus the term in the nth minus 2 position. The equation to solve for any term in the sequence is:
#Calculate fibonacci how to#
How to Calculate a Term in the Fibonacci Sequenceīecause each term in the Fibonacci sequence is equal to the sum of the two previous terms, to solve for any term, it is required to know the two previous terms.


 0 kommentar(er)
0 kommentar(er)
